什么是图
"图是由一些顶点和和一组能够连接2个顶点的边组成" ---《算法》
图的分类
无向图:连接顶点的连线叫 边, 只在意2个顶点是否连接,不在意谁连向谁。
有向图:连接顶点的连线叫 弧, 不仅在意2个顶点是否连接,还在意谁连向谁。
无向加权图:无向图的基础上,为边赋予一个数值,当做这个边的权重。
有向加权图:有向图的基础上,为弧赋予一个数值,当做这个弧的权重。
下面有具体的分析。
图的性质
1、元素构成的集合中的任意2个元素之间的关系是任意的的:可能相关联,也可能不相关。可能互相关联,也可能单向关联。
2、元素 之间无主次关系,所有元素 都是平等的 (peer)。
3、图中的顶点是不在意位置,或者顺序的。图只在意顶点之间的连接关系。
怎样表示图
①用一个集合保存图中的所有元素 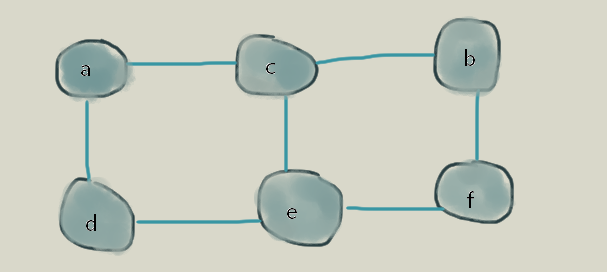


②用另一个集合保存所有元素之间的关联 关系(边,或者弧)
这个2个集合,就能确定一个图
下面举例说明。
无向图
若G表示一个图,则 :G = < V , E>
其中V代表图中的所有顶点(元素)构成的有限集合
集合E,表示图所有的关联关系(边or弧)。我们知道 图中2个节点的关系 是由2个顶点确定的,所以,集合E中的元素都是成对的顶点。
根据下图可以写出这两个集合
V = { a,b,c,d,e,f }
E = { (a,c) , (a,d ) , (c,e ) , ( c,b) , ( b,f ), (d,e) (e,f) }
V,存储所有的元素,E,存储元素之间的关联关系。
图中 a和c 有 关联,则E集合中有(a,c)这个元素。
可以发现,在下面这个图中,我们只强调2个元素之间是否有连接,而不在意是 谁连向谁,也就是连线只有 有无2种状态,没有方向,(a,c) 等价于(c,a) ,这就是无向图。

有向图
与无向图不同的是,有向图不仅在意是否关联,还强调关联的方向:c----->e e----->c 是不同的
同样我们写出V和E 2个集合
V = { a,b,c,d,e,f }
E = { <a,c> , <b,c > , <b,f>, <c,e > , <d,a>, <d,e> , <e,c> , <e,f> }
同时要注意:无向图中的关联关系 用 ( ) 圆括号表示 ,而有向图 中 用 < > 尖括号

一些术语解释
顶点(Vertex):图中的元素,叫做顶点
边(Edge):无向图中,顶点与顶点之间的连线
弧(Arc):有向图中,顶点与顶点之间有方向的连线
弧头:
弧尾 :

邻接点: 与这个顶点有直接关联的顶点
顶点的度: 与这个顶点 关联的边(弧)的数目
顶点的出度:有向图中,这个顶点向外发射多少弧,就是多少度
顶点的入度:有向图中,顶点接收其他顶点的弧的条数,就是多少度
有向图中:顶点的度 = 出度 + 入度
子图:若有G = <V , E > , G1 = <V1,E1> ,且 V1是V的子集,E1是E的子集,则 G1为G的子图
有圈图:允许顶点自己和自己关联
无圈图:不允顶点许自己和自己关联(不特殊说明,我们一般都是指无圈图)
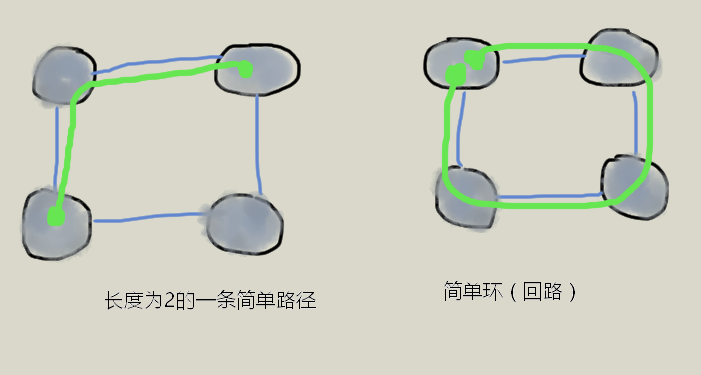
路径:从一个顶点到另一个顶点的通路,由边(弧)组成。边(弧)的条数,就是路径的长度
简单路径:通路中经过的顶点不重复。
简单环 :特殊的路径,从起点出发,再回到起点,形成的路径。经过的顶点不重复。
不特殊说明,一般我么研究的路径都是简单的。

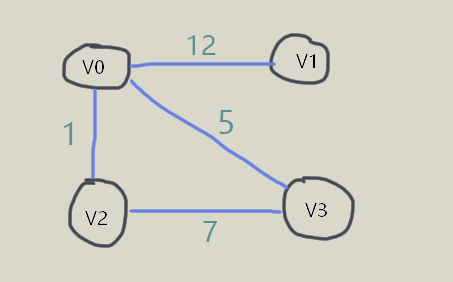
无向加权图和有向加权图(又叫无向网和有向网)
何为加权?
加权:为边(弧)分配权值(weight),这个权值的意义在与衡量 跨越2个顶点的某项指标。比如在一个地图上,A.B 2点 用打车的费用代表这2个顶点的权。

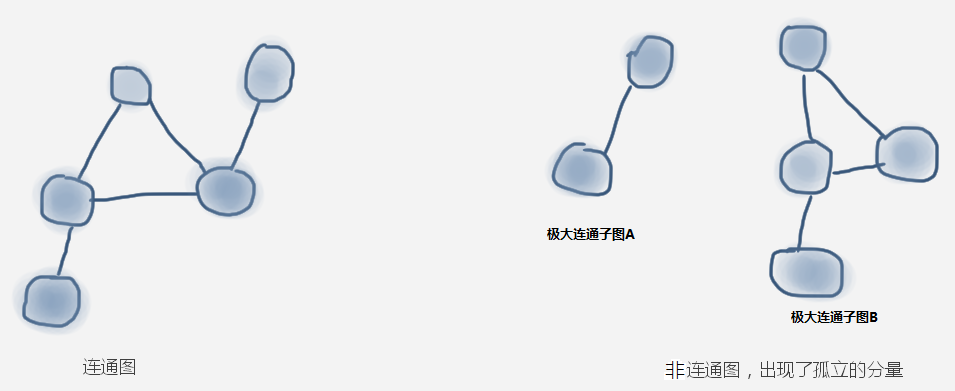
连通图与非连通图
连通图:无向图中,任意2个顶点之间,总有路径可以互通(不一定要是直达,中途可以借助一些顶点为跳板"转达")。完全图一定是连通图。
非连通图:整个图由 n 个现孤立 连通图组成。非连通图中的每一个孤立部分都是它的极大连通子图。
可以这样想:将一个图的顶点想象为念珠,边为连接念珠的细绳,如果随意提起一颗念珠,所有的念珠都会被提起来,就说明这个是连通图,否则不是。

连通分量:无向图中,每一个极大连通子图都叫一个连通分量。如上图右边,A是一个连通分量,B也是一个连通分量。
连通图的(最小)生成树: 图和树的一个很大的区别是,树中一定不能有环,但是图就没有这个要求了。一个树也是一个图。
一个连通图(注意这是前提)的生成树就是一个包含原图中所有顶点的树。
强连通图: 有向图中,任意2个顶点之间都有出,入的2种弧。
强连通分量:有向图中,极大(顶点数最多的)强连通图
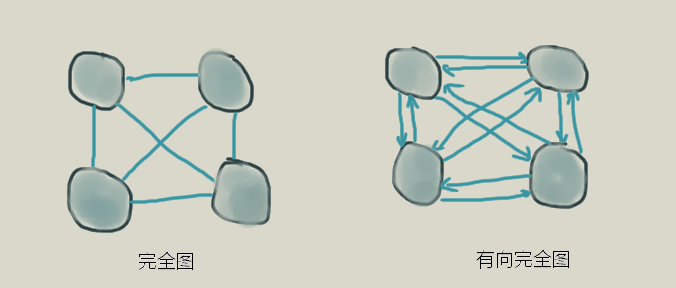
无向完全图 和 有向完全图
无向完全图
无向图中,每个顶点与其他顶点都有边相关联,则这个图就是(无向)完全图。
可知:有n个顶点的完全图的边为 : 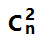 = 1/2 * n * (n-1)
= 1/2 * n * (n-1)
有向完全图
有向图中,每个顶点与其他顶点都有 出 和 入 2种 弧 ,则这个图就是有向完全图
可知:有n个顶点的有向完全图的弧为: 2* ( 1/2 * n * (n-1) ) = n * (n-1)
也可知:有n个顶点的无向图中,边数 L 满足 : 0<= L <= 1/2 * n * (n-1)
有n个顶点的有向图中,弧数 L 满足 : 0<= L <= n * (n-1)

下一站: